Content

• Intro
• Problem Description
  • Example Input/Output
• Approach
• Code
  • Final Code

Intro

If you are not familiar with this problem already, please check it out here. This is one of my favorite LC problems, so let’s dive into it!

Problem Description

Given an m x n 2D binary grid grid which represents a map of ‘1’s (land) and ‘0’s (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example Input/Output

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Approach

One important factor to solve problems effectively is the ability to extract the important keywords.

In our problem, the keyword that would help us come to a solution is adjacent. Blocks of land (i.e. the 1’s (ones)) are adjacent to each other. So if we are standing at a ‘1’ on the island, we can travel across the entire island by visiting neighboring, adjacent 1’s (ones).

If we travel through the grid until we find a 1, this means we are on an island, so we should increment the numberOfIslands by one. After incrementing it, we move on to the next cell on the grid. What if the next cell on the grid is also a 1? We should not consider this as a new island, instead, it should be part of the area of the previous island. This will lead to an important conclusion: at each cell with a value of 1, we need to visit all of its adjacent 1’s (ones) before we move across the grid looking for a new island.

Let’s visualize this. 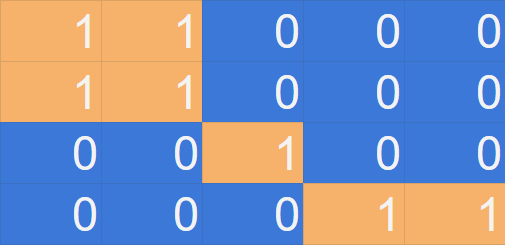Initial grid from example 1

Traversing the grid, nothing to the left, so we go right

‘1’ found to the left, traversing to the left

‘1’ back to where we started, there is 1 to the right, but if we go there, we’ll be in an infinite loop!

To resolve the infinite loop, we need to tell our algorithm not to visit a cell that we already examined before. One approach could be to store the indices of all the cells that we traversed in a unique set, and check whether the next cell we will visit has been visited in the past before each move. 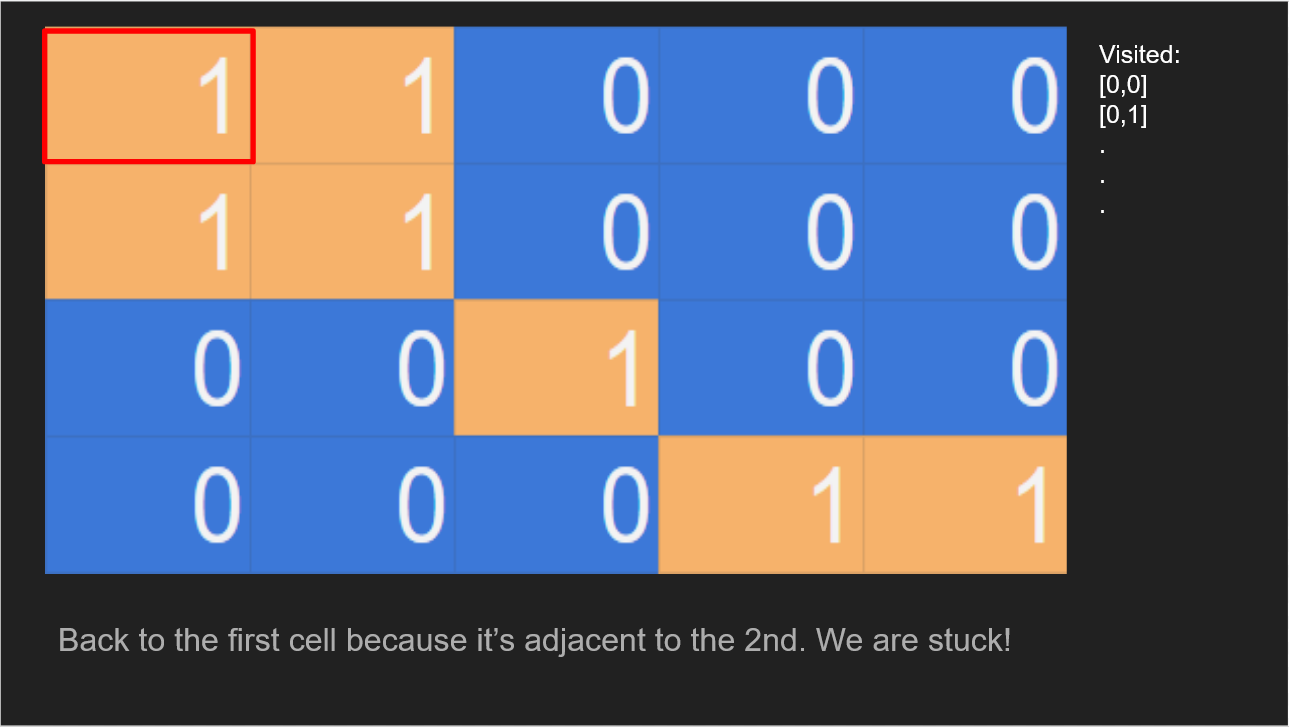Adding a visited set of unique indices to keep track of visited cells

However, this approach is computationally expensive!

We only need the number of islands we come across; we don’t need to know how many “cells” are there within each island. So while traversing, we can change the value of each 1, and it would not affect our solution at all. Since we do not have any adjacent islands (only adjacent cells), this approach will work fine.

Let’s visualize this again.

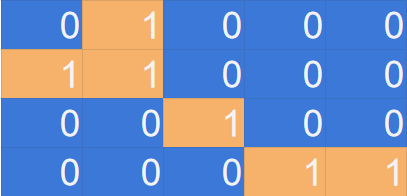After we visit the first cell, we set its value to ‘0’ because we don’t care about it anymore. Then we check its neighbors.

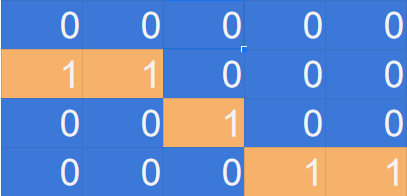After we visit the second cell, we set its value to ‘0’ because we don’t care about it anymore. Then we check its neighbors.

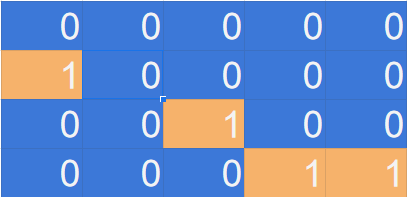After we visit the third cell, we set its value to ‘0’ because we don’t care about it anymore. Then we check its neighbors.

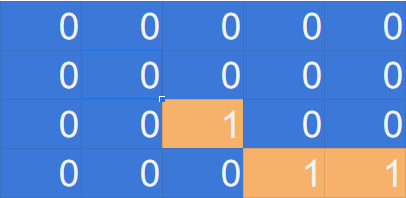After we visit the fourth cell, we set its value to ‘0’ because we don’t care about it anymore. No adjacent neighbors are equal to 1. This island is done, so we move on.

We will repeat what we have done above for each island until we reach the end of the grid.

Now let’s see how we’re going to do this in code.

Code

class Solution {
    public int numIslands(char[][] grid) {
        
        int numberOfIslands = 0;
        
        for(int row=0 ; row<grid.length ; row++) {
            for(int col =0 ; col<grid[0].length ; col++) {
                if(grid[row][col] == '1') {
                    numberOfIslands++;
                    traverseIsland(grid, row, col);
                }
            }
        }
        
        return numberOfIslands;
        
    }
}

The method numIslands is mostly a driver function that invokes traverseIsland, which - in fact - does most of the heavylifting.

private void traverseIsland(char[][] grid, int row, int col) {
    // These are the stopping conditions for the recursive method.
    // If we go outside the boundaries of the grid, or if we have a cell that's a '0' (water),
    // which means that there is no more land in this direction.
    if(row<0 || row>= grid.length ||
        col<0 || col>= grid[0].length ||
        grid[row][col] == '0')
        return;

    // If we reach here, it means that the current value in the cell is '1'.
    // We change its value because we don't care about it anymore.
    grid[row][col] = '0';

    // now we need to check whether the neighbors to the left, right, top, and bottom are part of the current island
    traverseIsland(grid,row,col-1);
    traverseIsland(grid,row, col+1);
    traverseIsland(grid,row-1, col);
    traverseIsland(grid,row+1, col);
}

Final Code

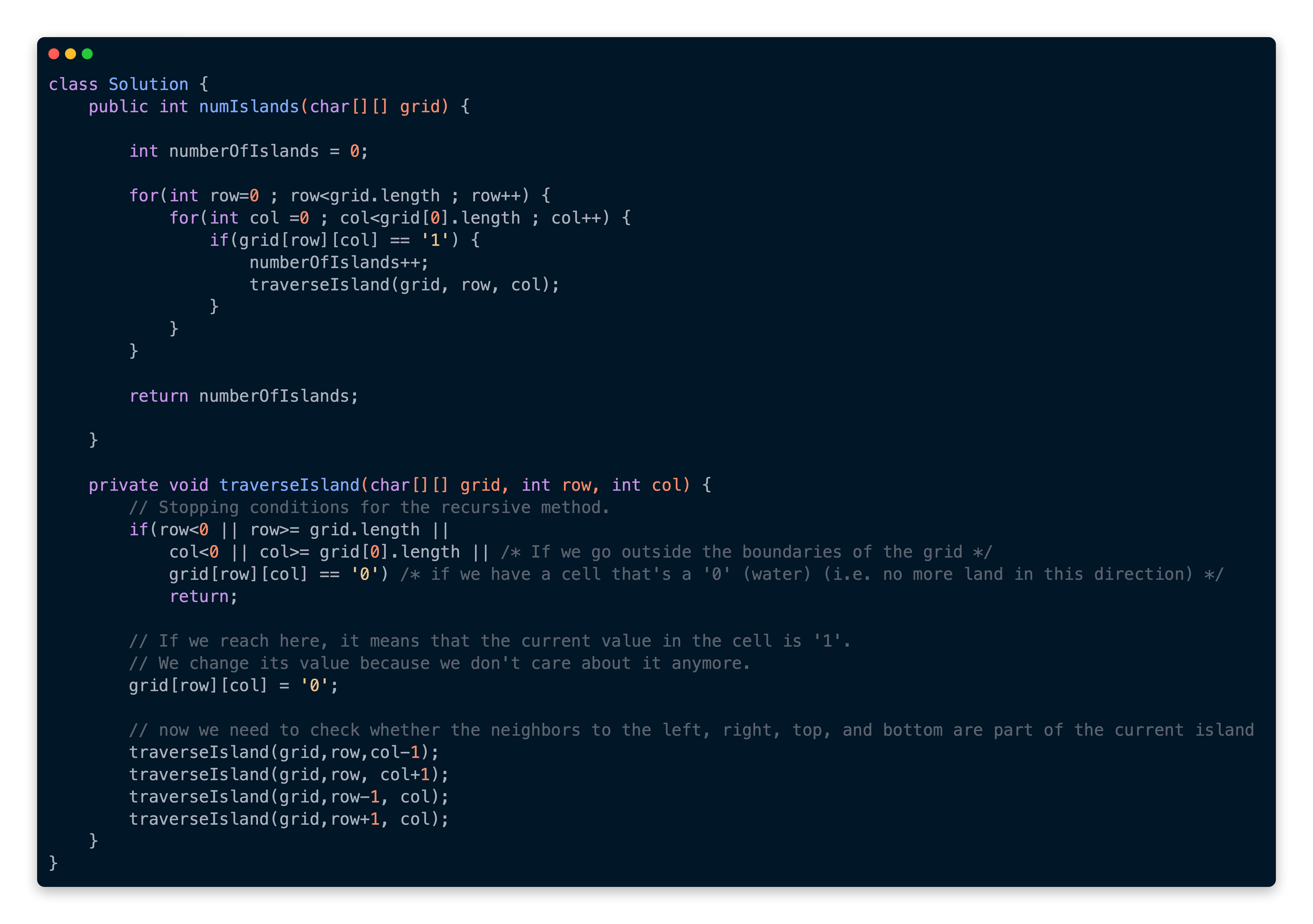This is how our final code is going to look.

I hope you enjoyed this tutorial.

Let me know what you’d like me to talk about in future articles by tweeting me